Abstract : A new module is added to SimPIMF. This module creates a series of modular coils defined as parametric polylines on a toroidal surface. The code optimises the modular coils following the same process already created for helical coils.
Graph 4 . Magentic surface defined by an orbit (cyan). Helical magnetic axis (yellow). The surfice in cyan shows the same helical shape (difficult to see here)
Graph 3 . Orbit corresponding to the helical magnetic axis.
Objective
The aim is to test if the calculation of simple modular coils with good confinement is possible. This will allow the continuation of the engineering design which depends on the style of coils (classical helical coils or modular coils).
Some time ago the idea of modular coils was abandoned because of the difficulty to calculate them without NESCOIL or a similar code.
General description
One adequate way to optimise coils is the use of codes style NESCOIL which starts from the definition of a plasma with good confinement and stability properties and calculate the modular coils from it. At the moment neither the process nor the code is available so the method described in [1] is followed.
The style of the modular coils is an extension of the one defined in [2]. This type of coils is similar to the modern coils calculated by NESCOIL or COILPLOT. For example the coils from Garabedian [3] [4] and Najmabadi [5] have some resemblance to the calculated here. However those coils are much more optimised and the winding surface is not circular for the best optimization. [6] has a good description of optimization.
Here the coils are generated by a sinusoidal function on the circular winding surface modified by 4 parameters. This is a simplification of a possible analysis by Fourier series which will take much longer to calculate. The parameters define the magnitude of twist in each of the 4 sinusoidal half-periods of the coil. Each twist intensification is interpolated from the four parameters. Another parameter defines the speed of turn of the coils on the surface.
The number of periods m=2, m=3 also have influence in the design.
The cases with lowest magnetic ripple, enough plasma size and less twist of coils are chosen. Each calculation of 625 cases lasts about 1 hour. The proportion of trapped particles will be calculated next.
Only the case m=2 is analysed. The case m=3 should be interesting and will be also considered.
This is only a rough calculation to decide about the existence of good magnetic surfaces. A finer run should be done later.
New addtions to the code
SimPIMF v2.1 adds a module to inject a series of particles from the X+ axis all in the same direction Y+ and uniformly distributed on the axis. The lower and upper X+ coordinate of the particle is near the chamber wall in order to obtain, if it exists, plasmas up to 50mm of diameter.
If there are particles that remain in the magnetic field they are used to calculate the averaged ripple of the total number of particles and the plasma size on the X+ axis.
It is supposed that there are not singular particles. For example a particle inside a volume of stable particles that escapes of the system. This is a sound supposition (~concentric magnetic surfaces and other reasons).
Usually 11 particles are injected.
The final selection of the best cases is done by ordering them in a spreadsheet.
Some examples
"CONTINUOUS" coils
In the first simulations the set of coils rotate continuously on the torus. This do not fullfil the condition of symmetry between half-periods, only the periods are identical but not necessarily symmetrical.
First the effect of the discrete number of modular coils is analysed.
The same effect happens in HF + TF coils but this was not analysed in [1].
Ripple from the number of coils
In modular "continuous" coils with unitarian parameters, m=2 and size of device like in [1] :
Number of coils : 8 ; Ripple = 0.31 at axis + 20mm
Number of coils : 10 ; Ripple = 0.23 at axis + 20mm
Number of coils : 12 ; Ripple = 0.19 at axis + 20mm
Number of coils : 16 ; Ripple = 0.17 at axis + 20mm
This "natural" ripple seems optimizable by the variation of the 4 parametes.
Optimization
Number of coils = 16 ; m=2
The general deformation of coils in this case is 0.15 in order to avoid superposition of coils. The case 0.2 is sometimes possible.
Intervals for optimization : Pitch1, 2, 3, 4 = [0.75 , 1.5]
2401 different structures analysed.
Ripple at magnetic axis + 10mm
Only one particle is simulated.
| m | Loop | Pitch 1 | Pitch 2 | IPitch 3 | Pitch 4 | Iota | Ripple | |
| A | 2 | 391 | 1.375 | 1.0 | 1.125 | 1.0625 | 0.176 | 0.082 |
This type of coils is improved in the next simulations
Modular "SYMMETRICAL " coils
In this system the coils have "stellarator symmetry" like in all normal modular coils [3] [4] [5] [6].
Optimization
Number of coils = 16 ; m=2
TF current= 3525A-turns
In the table :
Size is the diameter of the plasma in mm.
Ripple is the average ripple for the group of 11 particles that are analysed in each structure of coils.
Tor : Torsion = speed of turn of the coils. The value 1.3333 should be the best considering only geometrical uniformity.
Def : The general deformation of the coils. A value of 0.2 gives coils that sometimes intersect. 0.15 usually gives feasible coils.
Some case with very low plasma radius and even low ripple are ommited in the table
| m | Def. | Tor | Pitch 1 | Pitch 2 | IPitch 3 | Pitch 4 | Ripple | Size | |
| H | 2 | 0.15 | 1 | 1 | 1 | 1 | 1.5 | 0.048 | 20 |
| I | 2 | 0.15 | 1 | 1 | 1 | 2 | 1 | 0.044 | 15 |
| J | 2 | 0.15 | 1.33 | 0.75 | 0.75 | 1 | 1 | 0.109 | 35 |
| K | 2 | 0.15 | 1.33 | 0.75 | 0.5 | 1 | 1 | 0.105 | 25 |
| L | 2 | 0.15 | 1.6 | 1 | 1 | 1 | 1 | 0.113 | 45 |
| M | 2 | 0.15 | 1.6 | 0.75 | 1 | 1 | 1 | 0.104 | 30 |
| N | 2 | 0.15 | 1.16 | 1.63 | 1.25 | .875 | 1.63 | 0.033 | 20 |
| O | 2 | 0.15 | 1.16 | 1.63 | 1.25 | 0.5 | 1.63 | 0.055 | 30 |
| P | 2 | 0.15 | 1 | 1.25 | 0.5 | 1.5 | 0.75 | 0.034 | 15 |
| Q | 2 | 0.15 | 1 | 1.75 | 0.5 | 1.75 | 0.75 | 0.039 | 20 |
| R | 2 | 0.15 | 1 | 1.75 | 0.5 | 1.75 | 1 | 0.066 | 30 |
| S | 2 | 0.15 | 1.08 | 1 | 0.75 | 0.5 | 1.75 | 0.044 | 20 |
| T | 2 | 0.15 | 1.08 | 1.5 | 0.5 | 1.75 | 0.5 | 0.072 | 30 |
| U | 2 | 0.15 | 1.08 | 1.75 | 0.5 | 1.75 | 0.75 | 0.095 | 40 |
| V | 2 | 0.15 | 1.33 | 1.75 | 0.75 | 1 | 0.75 | 0.041 | 20 |
| W | 2 | 0.15 | 1.33 | 0.75 | 0.5 | 0.5 | 0.5 | 0.041 | 20 |
| X | 2 | 0.15 | 1.33 | 1.5 | 1 | 0.75 | 1.25 | 0.053 | 30 |
| Y | 2 | 0.15 | 1.33 | 1 | 1 | 0.75 | 1 | 0.070 | 40 |
| Z | 2 | 0.15 | 1.33 | 0.75 | 1.25 | 1 | 0.75 | 0.011 | 50 |
Case H & I :
Intervals for optimization: Pitch1, 2 = [0.5 , 1.0] Pitch3 , 4 = [1.0 , 2.0]
81 different structures analysed. The two best results appear in the table.
* This case is little sensitive to the changes in the shape of the coils. Half of the tested coils produce a wide plasma.
Case J & K :
Intervals: Pitch1 , 2 = [0.5 , 1.0] Pitch3 , 4 = [1 , 2]
81 different structures analysed.
*The torsion is 1.3333 which gives geometrical uniformity. However ripple seems a little higher than in case H&I (not totally comparable due to different plasma size)
Case L & M :
Intervals for optimization Pitch1, 2 = [0.5 , 1.0] Pitch3 , 4 = [1 , 2]
81 different structures analysed.
* There is over torsion here (1.6).
* This case is very sensitive to the changes in the shape of the coils. Only 1/7 of the cases have magnetic surfaces.
Case N & O :
Intervals for optimization Pitch1, 2 , 3, 4 = [0.5 , 2.0]
625 different structures analysed.
* Wide plasma and low ripple.
Cases P to U :
Intervals for optimization Pitch1 , 2 , 3, 4 = [0.5 , 1.75]
1296 different structures analysed.
* Most of the cases are chosen with the sum of the 4 parameters < 5. If possible in [4,5] to avoid very twisted coils.
* Highly twisted coils always achieve lower ripples for the same max. plama size but they are avoided in the table.
* Some regularities are observed in the "Pitch" of the table. This is similar to the increase of twist in some regions in modular stellarators. Among P, Q, R, T, U . In N, O, S
Cases V to Z :
Intervals for optimization Pitch1 , 2 , 3, 4 = [0.5 , 1.75]
1296 different structures analysed.
* They seem the best. Moreover this is the geometrical smooth case.
* 1040 cases out of 1296 have confined orbits, higher value than the other cases.
Position of the magnetic axis and Iota
* The magnetic axis is helical in most of the simulations. This is a pleasant surprise. Quasi-helical symmetries happen only in devices with helical axis (W7-X , HSX). Low ripple is related with little variation of B on a field line (only in strange cases this could be wrong). So here low ripple might be related to quasi-helical symmetry. .
The present code do not calculate the position of the magnetic axis. It is simple to obtain manually in particular cases.
The current code calculates Iota with difficulty in plasmas with helical axis. It is possible for outer surfaces. It will be improved.
Graphs
Some additional simulations are carried out for the case "X" in the table.
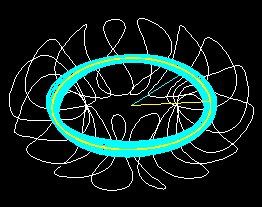
Graph 1 : The filamentary representation of the system of modular coils is shown. The helical magnetic axis and a magnetic surface is also displayed. The particle is trown from x =0.111+ 0.010 (magnetic axis is at x=0.111)
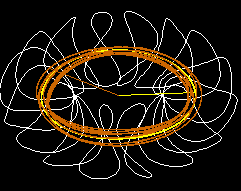
Graph 2 : The orbit of a particle on a rational surface is shown. It gives Iota=0.1421 by calculation. The figure reflects 7 repetitive paths. So the rational might be 1/7 = 0.1428 ~ 0.1421 . The particle is trown from x =0.111+ 0.01105
Graph 3 : It shows the helical axis of the magnetic confinement.
Graph 4 : The same magnetic surface and axis in Graph 1 from a lateral point of view.
Proportion of trapped particles
Not calculated here. It is a similar simulation as in [1] and very
related to ripple [1] [7].
Conclusions
* The values of ripple are much smaller than in [1] and [7], for helical or heliac devices. This is highly positive. However the reason is not clear. Perhaps the reason is the helical axis. The magnetic axis is coplanar in the cases in [1]. More study is necessary.
* There is already enough degree of freedom in the results in the table to optimize other important physical and engineering factors.
* Presently modular coils are the best option
for UST_1 stellarator and now it seems a better alternative to
classical stellarators with helical coils.
Further developments
The selected cases will be analysed (shape of magnetic surfaces, Iota ..). The final engineering design need to be defined.
References
[1] "Optimization of UST_1 for m=3, 4 and 5 periods. Minimization of trapped particles and ripple" , Vicente M. Queral . See “Past R&D" in this web
[2] K. Miyamoto . Nuclear Fusion 18 , pg 243. Cited in Dolan, pg 398
[3] "A TWO FIELD PERIOD CANDIDATE FOR ARIES-CS" P.R. Garabedian. Web
[4] "Compact stellarators with modular coils". Garabedian, PNAS , July 18, 2000 , vol. 97 , no. 15
[5] "Exploration of
Compact Stellarators as Power Plants"
Farrokh Najmabadi , 16th ANS TOFE
[6] "Physics and engineering design for wendelstein 7-X" Craig Beidler, G. Grieger , et al. Fusion Tech. 1989
[7]
"Electron cyclotron heating and current drive in the TJ-II
stellarator"
,
V Tribaldos, J A Jimenez, et
al .
Plasma Phys.
Control. Fusion 40 (1998)
Graph 1 . Filamentary representation of the modular coils (white). Magnetic surface (orbit in cyan). Helical magnetic axis (yellow)
Graph 2 . Orbit (red) on a rational magnetic surface.
Graph 1 . Filamentary representation of the modular coils (white). Magnetic surface (orbit in cyan). Helical magnetic axis (yellow)
Graph 2 . Orbit (red) on a rational magnetic surface.
Last Update 9-1-2006